Stable Diffusion, How Does It Work?

Stable Diffusion, How Does It Work?

Stable diffusion is a latent diffusion model, a neural network specialized in denoising images. It is a generative model, more specifically, a text-to-image model, which can create images similar to what it has been exposed to on the training dataset, based on the text prompts.

We have mentioned that Stable Diffusion is a neural network that denoises images. But how does it denoise an image, or how is a noisy image obtained in the first place? To understand, we should look into forward diffusion and reverse diffusion processes, which are not exactly what Stable Diffusion uses, but are good starting points.

In the forward diffusion process, we apply a small amount of Gaussian noise at every step, eventually obtaining a noise image.

In the reverse diffusion process, we attempt to recover the original image from the noise image. However, as the conditional probability value resulting from the forward diffusion process cannot be calculated, instead, we attempt to predict it with another neural network called noise predictor. What the noise predictor does is basically, generate a random Gaussian noise image, subtract the estimated noise from it, generating a less noisy image. Then, for a specific number of steps, this process is repeated, eventually obtaining a similar image to the image from the training dataset.

As can be seen, the reverse diffusion process yielded a different image, yet it is similar to the sample image that went through the forward diffusion process. It is important to notice that these processes demonstrate that neural networks do not simply crop and merge images present in the training dataset, but rather create similar images.

As we have mentioned, these processes are not exactly the algorithms behind Stable Diffusion. The reason is that, dealing with images, or more spesifically, with image spaces, is costly. With thus far established processes, it would be practically impossible to train a neural network with high quality images. We should, then, turn our attention to an improvement over this process. We have thus far focused on the term diffusion in the initial definition. Then, we should now focus on the other term in the definition, namely, latent. With the term latent, we mark our migration from the image spaces to the latent spaces.

Latent spaces offer a great improvement on image spaces as they are smaller than image spaces, thanks to their representation with structures called tensors rather than pixels. The question might be asked, then, cannot we readily represent an image as a tensor, and if we do, what will it yield any advantage for us? The answer is that, yes, we can represent an image as a tensor, but doing so carelessly will not gain us any advantage whatsoever.

As it is often the case in the information theory, we want to convey more information while lowering the costs. That is exactly what we are trying to achieve with latent spaces. So, how do we go about the process of migration from image spaces to smaller latent spaces? First lets establish that, for our purposes, that is, generating an image of a honey badger, a human being, a building, a star, or even a dragon, we do not mind losing some information. What is meant by losing some information is representing high dimensional datasets with their low dimensional latent manifolds. The reason is that, macroworld, that is, the world as we see it, is highly regular. Thanks to this regularity, it is possible to teach a neural network to compress an image with possible information loss but no meaning loss. The component that we have talked about, which can encode an image into a latent space, and decode a latent space to obtain an image, is called a variational autoencoder.

The latent space dimensions grow or shrink based on the size of the image to be generated. For Stable Diffusion, the base size is 512 x 512, and the latent space has dimensions 4 x 64 x 64. If we want to generate an image of size 1024 x 512, the dimensions become 4 x 128 x 64. If we want to generate an image of size 1024 x 256, the dimensions become 4 x 128 x 32. Please notice that, 4 x 64 x 64 is 48 times smaller than 3 x 512 x 512, a 48 times compression!

Now that we have established both of the terms in the initial definition, lets focus our attention to both of them at the same time. We have understood how the forward diffusion and reverse diffusion processes work for image spaces, and we have also understood how we migrate from image spaces to latent spaces. So, lets now talk about how to apply the forward diffusion and reverse diffusion processes to latent spaces.

In the forward diffusion process, again, we apply a small amount of Gaussian noise at every step, eventually obtaining a noise image.

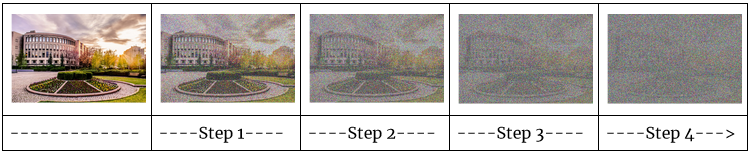
In the reverse diffusion process, again, we attempt to recover the original image from the noise image. However, this time, what the noise predictor does is, generate a random Gaussian noise latent tensor, subtract the estimated noise from it, generating a less noisy latent tensor. Then, for a specific number of steps, this process is repeated, eventually obtaining a similar latent tensor to the latent tensor of the image from the training dataset.

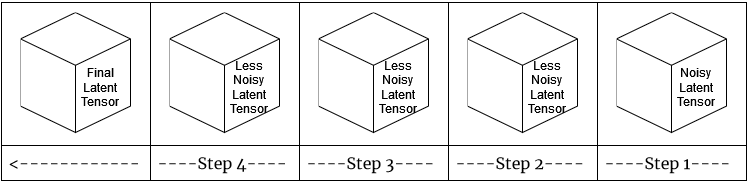
And of course, the variational autoencoder turns this latent tensor into a similar image to the image from the training dataset.

Please keep in mind that, because the noisy latent tensor we create at the first step is random, and because our final latent tensor depends on it, we will get different final results everytime.

(To be continued..)